In the past several years, I have increasingly run into arguments, something to the effect of
``
1) US interest rates ebb and flow with some kind of cycle,
2) when it goes down, cheap US dollar is made available to the rest of the world,
3) which developing countries, including countries like China, excessively consume (borrow),
4) and this essentially becomes pretty much a decoy because
5) when Fed increases rates, capital outflows from those countries almost instantaneously, creating capital flights.
6) Knowing this mechanism, US government is taking advantage of it to `tame' rising powers.''
I don't know who's spreading this kind of thing, but this is just a BS.
True, it's a straightforward story, that contains some drama appealing to people.
But in this story, only 1) and 2) are consistently true and, thus, the inference 4) and 6) that are based on them are just wrong.
3) is wrong, because `excessively consumption' happens only rarely and typically not in the countries that can pose any significant politco-economic threat to US. (e.g., Brazil).
5) reversal of capital flows does happen, but that hasn't necessarily created capital flights.
Most importantly, the big assumption this false story is rooted on is absolute non-sense.
Fed enjoys significant degrees of political independence from the US government, as is a typical central bank of an advanced economy (otherwise, inflation fighting is difficult). It does not accommodate the WH's foreign policy goals that diligently! In other words, whatever happens to emerging markets as a consequence of rate hikes, it's more likely to be an unintended one rather than deliberately orchestrated one.
Monday, February 15, 2016
Monday, February 8, 2016
[method ramble #2] 3D plotting in Stata.
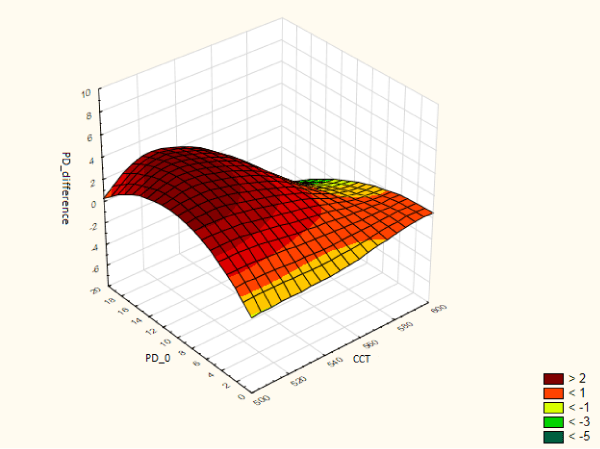
So 2-way multiplicative interaction terms are actually best illustrated by 3D `area' plots.
The 2-dimensional plots that I've been using (and most of us have been using) are actually more of a snap shot of this. The downside of 2-D plots is of course you need to make compromise. Arbitrary decisions.
For example, consider a simple linear model with a 2-way multiplicative interaction term,
f = xb1 + yb2 + xyb3 + e,
where both x and y are continuous variable.
To present a `marginal effect' of x, that is x's effect on f conditional on y, one need to take a certain difference value (most typically dy/dx). Then you make the case that `when 1 unit changes in x, f changes this much where y values are such and such'. This assumes that x's effect on f is strictly linear: it doesn't matter the change in x we are assuming in the 2d marginal effect figure is from 1 to 2 or 101 to 102. dy/dx assumes it's essentially the same 1-unit change.
Most often, of course, this isn't very realistic. I mean, think of diminishing marginal returns.
One needs to show the whole picture of the structure between f, x, and y just like the picture above to fully explain their relationship.
I know Matlab does it pretty well. Indeed the picture above is generated by Matlab (I believe). But I don't want to learn another package.
Stata has some functions and I tried them today.
One was _graph3d_.
The logic is simply: you have x y and z variables and locate each data point based on them.
The picture I ended up having using my exchange rate regime choice data, though, looks ugly as hell.
This isn't no post-estimation command but I used it as though it was (using predicted values of the DV).
There were, of course, some options to apply, but essentially it does a poor job showing the relationship between variables. Granted, it not like _marginsplot_ where a certain relationship is assigned and simulated, but what was advertised was much more appealing than this ugly picture.
What could've been most useful would be 3d equivalent of _marginsplot_.
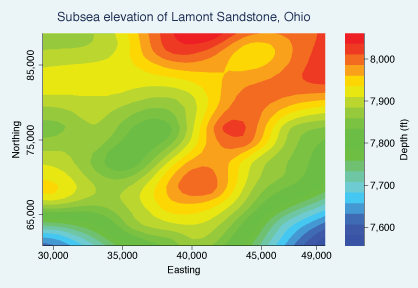
Another option, which I see more often these days, is _gr twoway contour_. It should generate something like this:
The figure surely does take into account multi-dimensional variation of data and in some ways much more effective in doing that than 3-d graphs do. It took, however, forever for my macbook pro to generate this with my data (obs=1,510). I needed to go back and forth quite a bit, and if I need to spend an hour every time, this isn't feasible.
-surface- was the third one that I tried. It seemed to have all the same problems that _graph3d_ had. More importantly, it approximates the values when the variable is continuous.
So I gave up there. Spending more than a whole afternoon on a marginally fancy graph that I may or may not use for the paper I'm working on is just insane, I thought.
For now, I would just show two dy/dxs: 1) x's marginal effect conditional on y and 2) y's marginal effect conditional on x.
The 2-dimensional plots that I've been using (and most of us have been using) are actually more of a snap shot of this. The downside of 2-D plots is of course you need to make compromise. Arbitrary decisions.
For example, consider a simple linear model with a 2-way multiplicative interaction term,
f = xb1 + yb2 + xyb3 + e,
where both x and y are continuous variable.
To present a `marginal effect' of x, that is x's effect on f conditional on y, one need to take a certain difference value (most typically dy/dx). Then you make the case that `when 1 unit changes in x, f changes this much where y values are such and such'. This assumes that x's effect on f is strictly linear: it doesn't matter the change in x we are assuming in the 2d marginal effect figure is from 1 to 2 or 101 to 102. dy/dx assumes it's essentially the same 1-unit change.
Most often, of course, this isn't very realistic. I mean, think of diminishing marginal returns.
One needs to show the whole picture of the structure between f, x, and y just like the picture above to fully explain their relationship.
I know Matlab does it pretty well. Indeed the picture above is generated by Matlab (I believe). But I don't want to learn another package.
Stata has some functions and I tried them today.
One was _graph3d_.
The logic is simply: you have x y and z variables and locate each data point based on them.
The picture I ended up having using my exchange rate regime choice data, though, looks ugly as hell.
This isn't no post-estimation command but I used it as though it was (using predicted values of the DV).
There were, of course, some options to apply, but essentially it does a poor job showing the relationship between variables. Granted, it not like _marginsplot_ where a certain relationship is assigned and simulated, but what was advertised was much more appealing than this ugly picture.
What could've been most useful would be 3d equivalent of _marginsplot_.
Another option, which I see more often these days, is _gr twoway contour_. It should generate something like this:
The figure surely does take into account multi-dimensional variation of data and in some ways much more effective in doing that than 3-d graphs do. It took, however, forever for my macbook pro to generate this with my data (obs=1,510). I needed to go back and forth quite a bit, and if I need to spend an hour every time, this isn't feasible.
-surface- was the third one that I tried. It seemed to have all the same problems that _graph3d_ had. More importantly, it approximates the values when the variable is continuous.
So I gave up there. Spending more than a whole afternoon on a marginally fancy graph that I may or may not use for the paper I'm working on is just insane, I thought.
For now, I would just show two dy/dxs: 1) x's marginal effect conditional on y and 2) y's marginal effect conditional on x.
[method ramble #1] To start.
So it's been a while.
There hasn't simply been an issue I seriously though that I must write something about.
Or more honestly, I have grown increasingly lazier.
Instead of sporadically feeling guilty about a defunct blog, I decide to spend the space on something slightly, like really slightly, more useful.: my method.
I am not a methodologist. I like quant methods. I believe in it. But I simply wasn't trained as a methodologist and don't plan to be in the near future. But at the same time, it's been my obsession to rigorously `spend' the outcomes that methodologists `produced' because doing so seems to be leading to a better science (as well as looking cooler).
I've got a lot to catch up on that front. Methodological advancement political science as a social science field has made is more than astonishing particularly in the past 3-4 years--during which I depleted the usefulness of my outdated method skills.
A few things that I need to really LEARN pretty soon:
1. difference-in-difference
I would've used it for my dissertation if I knew it existed. I was too lazy to know that. I think I get the math, but need to get the hang of it if I want to use it to expand my speculative attacks project.
2. regression discontinuity
Again, I get the math. But need to learn the language.
3. text scraping
There are a few folks who have already well established ways in which researchers scrap data from various sources. I need to have an `original dataset' at some point and this seems to be the closest thing to tap into for now.
4. matching and other causality stuff
I mean, it's a sure thing.
These are long-term goals though. Each task wouldn't really take much time, but I am grappling with a lot of stuff and with the snowcolypse in the DC area, I have been taken hostage at home with kids for the whole first month of the year.
So mostly what I'll be posting here would be day-to-day issues and most likely frustrations I have related to methods (BROADLY DEFINED).
There hasn't simply been an issue I seriously though that I must write something about.
Or more honestly, I have grown increasingly lazier.
Instead of sporadically feeling guilty about a defunct blog, I decide to spend the space on something slightly, like really slightly, more useful.: my method.
I am not a methodologist. I like quant methods. I believe in it. But I simply wasn't trained as a methodologist and don't plan to be in the near future. But at the same time, it's been my obsession to rigorously `spend' the outcomes that methodologists `produced' because doing so seems to be leading to a better science (as well as looking cooler).
I've got a lot to catch up on that front. Methodological advancement political science as a social science field has made is more than astonishing particularly in the past 3-4 years--during which I depleted the usefulness of my outdated method skills.
A few things that I need to really LEARN pretty soon:
1. difference-in-difference
I would've used it for my dissertation if I knew it existed. I was too lazy to know that. I think I get the math, but need to get the hang of it if I want to use it to expand my speculative attacks project.
2. regression discontinuity
Again, I get the math. But need to learn the language.
3. text scraping
There are a few folks who have already well established ways in which researchers scrap data from various sources. I need to have an `original dataset' at some point and this seems to be the closest thing to tap into for now.
4. matching and other causality stuff
I mean, it's a sure thing.
These are long-term goals though. Each task wouldn't really take much time, but I am grappling with a lot of stuff and with the snowcolypse in the DC area, I have been taken hostage at home with kids for the whole first month of the year.
So mostly what I'll be posting here would be day-to-day issues and most likely frustrations I have related to methods (BROADLY DEFINED).
Subscribe to:
Posts (Atom)