A paper topic I've been thinking about in the past several years is Anti-authoritarianism around the world and its decline (that is, the rise of authoritarianism). As always, procrastination got in my way and I really haven't done anything on it. Recently, perhaps because of the election, it seems like an outcry of the rising authoritarianism in developed societies is not very uncommon. While I thought the argument has its merit, I wasn't really thinking of looking at the data even though I had a variable (the name is, you know, "anti-authoritarianism"), part of which was a central dependent variable of one of my published articles.
In my attempt to overcome Thanksgiving food coma this afternoon, I plotted a cross-national bar graph for this variable.
The variable antiauth captures individuals' Anti-authoritarianism (opposition to a military- or strongman rule) and each bar represents national average of the variable in each 'wave' of the Survey.
Both United States (yellow) and South Korea (green) showed their strongest anti-authoritarianism in the 1990s, which subsequently declined significantly in the 2000s. Recent presidential election results in both countries should make a certain amount of sense. To be fair, I didn't run numbers in any systematic way to see if these differences are actually statistically significant (yet).
I should really start working on this (after submitting what I've been working on, that is).
Saturday, November 26, 2016
Wednesday, November 16, 2016
Presentation Template
So we're getting closer to the end of the semester, which means there should be a lot of student presentations going on. In my GLOA 605, which is an MA-level interdisciplinary research method class, this is a big deal. For two weeks, students present their research projects. Having taught this class before, I noticed (and found it somewhat inconvenient) 1) that they have very different styles of presentation which sometimes undermines fair grading and 2) that many students had never presented their work in a professional manner (!) and thus messed up with time management due to poor structure of the slides. That led me to make a template that everybody in class has to adhere to. It might sacrifice their creativity a little bit, but it's a formal training through which everybody is expected to garner certain types of skills.
Monday, September 26, 2016
Why does the recovery in the developed world not translate into the growth of the developing world?
Short Answer: the recovery in the developed does not mean the recovery of their demand for imported goods. A, rather old, report from the UNCTAD provides us with a very intuitive graph. The positive associations between the growth of the North and the growth of exports of the South (which is considered a major conduit for their desperately needed growth) had disappeared in the 2012-3 when the recession took finally took its toll.
Analysts should (and must) have known this coming because this shift had a long way to come; and yet, not much of preparedness have we witnessed. Indeed, the disastrous Hanjin bankruptcy would have been negated, if not avoided, if this sort of intuition was reflected in policymaking.
Friday, April 22, 2016
What I am going to talk about Monday.
Until very recently, I had been declining the request to give a talk about Asia for various reasons. Sometimes the schedule simply didn't work out. Sometimes I had absolutely no idea about the topic. But then I felt pretty bad about refusing to go all this time and finally accepted participate in a student-organized project.
I still don't know what I will be talking about. but this is the slides (will be revised a lot, probably). I really don't think there has been any `pivot'. But the underlying conditions suggest that Asian countries will have to make some choices pretty soon. And the data suggests that keeping status quo (not really using more RMB) would be the right choice.
I still don't know what I will be talking about. but this is the slides (will be revised a lot, probably). I really don't think there has been any `pivot'. But the underlying conditions suggest that Asian countries will have to make some choices pretty soon. And the data suggests that keeping status quo (not really using more RMB) would be the right choice.
Wednesday, April 13, 2016
[book review] Demanding Devaluation by David Steinberg
In Demanding Revolution, David Steinberg proposes a convincing theoretical framework, namely,``conditional preference theory'', to answer the question, `why undervaluation is so rare despite its unequivocal economic benefit?'. He suggests that strong manufacturing sectors support undervaluation when and only when the cost the policy incurs to them is reduced by the government. These costs, including increasing wage levels and imported input costs as well as decreasing access to credits, can be reduced when 1) financial institutions are controlled by governments (such that banks are forced to provide cheap credits -- ``financial repression'') and/or 2) labor rights are limited (such that upward wage pressures are suppressed).
The empirical evidence he presents lends strong support to this framework. Using a mixture of quantitative and qualitative evidence, he shows that undervaluation is most likely in countries where 1) manufacturing sector accounts for large parts of the national economy, 2) labor rights are limited, and 3) banks are, at least partially, nationalized. While the quantitative evidence neatly illustrates this evidence in a cross-sectional time-series manner (although I believe Figure 2.3 can be drawn better), the beauty of the empirical analysis of the book is in the case studies. Of the five country cases studied, China and Korea confirms one side of the story, namely that sustained (though intermittently interrupted) periods of undervaluation was made possible by strictly controlled labor and banks combined with large manufacturing sectors. The cases of Argentina and Mexico, on the other hand, illustrate the prevalence of overvaluation when the condition present in China and Korea are absent (and the policy debates were overwhelmed by extraordinary levels of inflations) even though manufacturing sectors were fairly strong. The Iranian case represents a rather odd scenario where manufacturing sector is weak and commodity export is dominant in the national economy.
While I thoroughly enjoyed the book, a few aspects of it struck me as unclear, asking for further investigations. First, what was the role of the state, particularly in the cases of China and Korea? The conditional preference theory essentially is interest group theory, assuming that the strong interest groups' preference translates into policies without much interference of the state. But the very conditions that enabled undervaluation in these cases--nationalized banks and controlled labor--is the products of strong, autonomous states. Indeed manufacturing sectors were nurtured by states in its infant stages and elevated to the `strong' status through deliberate government actions; undervaluation was one of those. Granted, in the later stages, that is the 1990s for Korea and 2000s for China, industrialists outgrew the influence of the state and rather dictated exchange rate policies in some ways. This was not true, however, for the majority of the times that the book covers. (To be fair, the author does address this issue here and there, but I think this state-society(business) issue needs to be more seriously handled, preferably in the theory section)
Second, in a similar vein, the external factors are not modeled in the conditional preference theory. The big difference between China/Korea and Argentina/Mexico, however, is their industrialists' access to foreign credits. In the former, individual firms' foreign borrowing had been substantially limited until financial liberalization (which really hasn't come to China even these days) and the degree to which the global interests rates influenced domestic markets was much narrower in these countries than in Argentina and Mexico. Again, the book does explain this part in the empirical section, but more as a sideway show that occasionally conditions each state's policy choices, not as a main independent variable.
Overall, the book significantly extends our understanding of monetary policies of developing countries. The literature does not really go beyond ``competent Asian states = undervaluation / incompetent Latin American-African states = overvaluation''. The book provides much more in-depth theorizing with convincing empirical evidence. I would use this for my graduate seminar.
Monday, March 7, 2016
Got some result for my reserve paper.
The paper was presented in MPSA2014 and ISA2014. But I had been just sitting on it until recently. The tenure anxiety got me re-working on it. After a number of hiccups (such as finding nonstationarity in the data because I forgot to consider the trend; yeah, shame on me), now I got a pretty robust result (translation: robust to FE :)).
Here's the marginal effect graph:
Here's the marginal effect graph:
I will come back to this when the theory is ``calibrated''.
[method ramble #3] zinb and TSCS
Recently, I've been working on a project on the relationship between inequality and social unrests (riots and demonstrations). The whole paper rests upon a conditional hypothesis:
y*_#riots = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (1)
y*_#demos = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (2),
where y* is a latent variable for riots (and demonstrations). An MLE function, of course, is necessary given that the latent continuous y* is not observed and instead we have data that counts the NUMBER of riots (say, y_#riots) and demonstrations (say, y_#demos) in a given country-year. So far, very straightforward.
Negative binomial regression is the answer. The current Stata estimator (_xtbgreg) takes care of time-series cross-section (TSCS) data pretty efficiently.
A problem arises when there are too many zeros.
The error term e may not be iid, however, when there's a systematic reason why y_#riots (and y_#demos) has so many zeros. In other words,
if equation (1) and (2) is affected by logit functions:
y(ritos |p=1) = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (3)
y(demos |p=1) = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (4),
then the results of (1) and (2) are likely biased.
Zero inflated negative binomial (zinb) is the way to go; but the current estimators do not deal with take into account the TSCS structure of data. The result might very well be biased.
So far a reasonable solution I've found would be something to the effect of a bunch of pair-wise comparisons like this. It makes a lot of computational sense, but I don't think it's compelling enough to convince any reviewers.
I googled quite a bit in search of a new estimator and found this one. It seems reasonable, but how stable it is hasn't been proven.
More practical solution I can think of particularly for fixed effects would be including country-year dummies in the 'inflate' equation. Whether or not the event occurs at all, I think, is much more driven by country-year heterogeneity than how often it does (for most political event, that is).
Of course, zinb fits data, but without 'recognizing' it is time series. Nonetheless a number of papers are published using zinb on TSCS data.
y*_#riots = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (1)
y*_#demos = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (2),
where y* is a latent variable for riots (and demonstrations). An MLE function, of course, is necessary given that the latent continuous y* is not observed and instead we have data that counts the NUMBER of riots (say, y_#riots) and demonstrations (say, y_#demos) in a given country-year. So far, very straightforward.
Negative binomial regression is the answer. The current Stata estimator (_xtbgreg) takes care of time-series cross-section (TSCS) data pretty efficiently.
A problem arises when there are too many zeros.
The error term e may not be iid, however, when there's a systematic reason why y_#riots (and y_#demos) has so many zeros. In other words,
if equation (1) and (2) is affected by logit functions:
y(ritos |p=1) = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (3)
y(demos |p=1) = b1*Gini + b2*d.Unemployment + b3*Gini*d.Unemployment + e ...... (4),
then the results of (1) and (2) are likely biased.
Zero inflated negative binomial (zinb) is the way to go; but the current estimators do not deal with take into account the TSCS structure of data. The result might very well be biased.
So far a reasonable solution I've found would be something to the effect of a bunch of pair-wise comparisons like this. It makes a lot of computational sense, but I don't think it's compelling enough to convince any reviewers.
I googled quite a bit in search of a new estimator and found this one. It seems reasonable, but how stable it is hasn't been proven.
More practical solution I can think of particularly for fixed effects would be including country-year dummies in the 'inflate' equation. Whether or not the event occurs at all, I think, is much more driven by country-year heterogeneity than how often it does (for most political event, that is).
Of course, zinb fits data, but without 'recognizing' it is time series. Nonetheless a number of papers are published using zinb on TSCS data.
Monday, February 15, 2016
FED interest changes as a tool for coercion?
In the past several years, I have increasingly run into arguments, something to the effect of
``
1) US interest rates ebb and flow with some kind of cycle,
2) when it goes down, cheap US dollar is made available to the rest of the world,
3) which developing countries, including countries like China, excessively consume (borrow),
4) and this essentially becomes pretty much a decoy because
5) when Fed increases rates, capital outflows from those countries almost instantaneously, creating capital flights.
6) Knowing this mechanism, US government is taking advantage of it to `tame' rising powers.''
I don't know who's spreading this kind of thing, but this is just a BS.
True, it's a straightforward story, that contains some drama appealing to people.
But in this story, only 1) and 2) are consistently true and, thus, the inference 4) and 6) that are based on them are just wrong.
3) is wrong, because `excessively consumption' happens only rarely and typically not in the countries that can pose any significant politco-economic threat to US. (e.g., Brazil).
5) reversal of capital flows does happen, but that hasn't necessarily created capital flights.
Most importantly, the big assumption this false story is rooted on is absolute non-sense.
Fed enjoys significant degrees of political independence from the US government, as is a typical central bank of an advanced economy (otherwise, inflation fighting is difficult). It does not accommodate the WH's foreign policy goals that diligently! In other words, whatever happens to emerging markets as a consequence of rate hikes, it's more likely to be an unintended one rather than deliberately orchestrated one.
``
1) US interest rates ebb and flow with some kind of cycle,
2) when it goes down, cheap US dollar is made available to the rest of the world,
3) which developing countries, including countries like China, excessively consume (borrow),
4) and this essentially becomes pretty much a decoy because
5) when Fed increases rates, capital outflows from those countries almost instantaneously, creating capital flights.
6) Knowing this mechanism, US government is taking advantage of it to `tame' rising powers.''
I don't know who's spreading this kind of thing, but this is just a BS.
True, it's a straightforward story, that contains some drama appealing to people.
But in this story, only 1) and 2) are consistently true and, thus, the inference 4) and 6) that are based on them are just wrong.
3) is wrong, because `excessively consumption' happens only rarely and typically not in the countries that can pose any significant politco-economic threat to US. (e.g., Brazil).
5) reversal of capital flows does happen, but that hasn't necessarily created capital flights.
Most importantly, the big assumption this false story is rooted on is absolute non-sense.
Fed enjoys significant degrees of political independence from the US government, as is a typical central bank of an advanced economy (otherwise, inflation fighting is difficult). It does not accommodate the WH's foreign policy goals that diligently! In other words, whatever happens to emerging markets as a consequence of rate hikes, it's more likely to be an unintended one rather than deliberately orchestrated one.
Monday, February 8, 2016
[method ramble #2] 3D plotting in Stata.
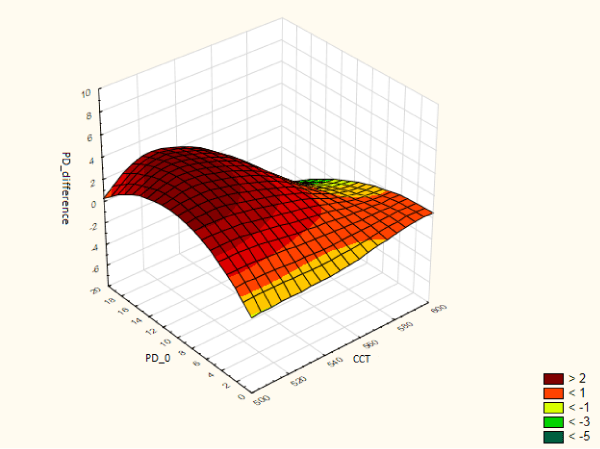
So 2-way multiplicative interaction terms are actually best illustrated by 3D `area' plots.
The 2-dimensional plots that I've been using (and most of us have been using) are actually more of a snap shot of this. The downside of 2-D plots is of course you need to make compromise. Arbitrary decisions.
For example, consider a simple linear model with a 2-way multiplicative interaction term,
f = xb1 + yb2 + xyb3 + e,
where both x and y are continuous variable.
To present a `marginal effect' of x, that is x's effect on f conditional on y, one need to take a certain difference value (most typically dy/dx). Then you make the case that `when 1 unit changes in x, f changes this much where y values are such and such'. This assumes that x's effect on f is strictly linear: it doesn't matter the change in x we are assuming in the 2d marginal effect figure is from 1 to 2 or 101 to 102. dy/dx assumes it's essentially the same 1-unit change.
Most often, of course, this isn't very realistic. I mean, think of diminishing marginal returns.
One needs to show the whole picture of the structure between f, x, and y just like the picture above to fully explain their relationship.
I know Matlab does it pretty well. Indeed the picture above is generated by Matlab (I believe). But I don't want to learn another package.
Stata has some functions and I tried them today.
One was _graph3d_.
The logic is simply: you have x y and z variables and locate each data point based on them.
The picture I ended up having using my exchange rate regime choice data, though, looks ugly as hell.
This isn't no post-estimation command but I used it as though it was (using predicted values of the DV).
There were, of course, some options to apply, but essentially it does a poor job showing the relationship between variables. Granted, it not like _marginsplot_ where a certain relationship is assigned and simulated, but what was advertised was much more appealing than this ugly picture.
What could've been most useful would be 3d equivalent of _marginsplot_.
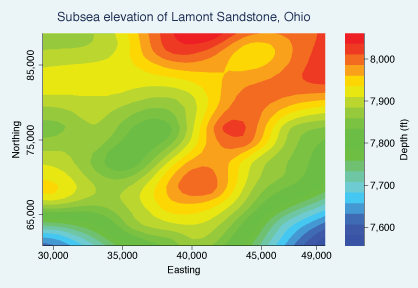
Another option, which I see more often these days, is _gr twoway contour_. It should generate something like this:
The figure surely does take into account multi-dimensional variation of data and in some ways much more effective in doing that than 3-d graphs do. It took, however, forever for my macbook pro to generate this with my data (obs=1,510). I needed to go back and forth quite a bit, and if I need to spend an hour every time, this isn't feasible.
-surface- was the third one that I tried. It seemed to have all the same problems that _graph3d_ had. More importantly, it approximates the values when the variable is continuous.
So I gave up there. Spending more than a whole afternoon on a marginally fancy graph that I may or may not use for the paper I'm working on is just insane, I thought.
For now, I would just show two dy/dxs: 1) x's marginal effect conditional on y and 2) y's marginal effect conditional on x.
The 2-dimensional plots that I've been using (and most of us have been using) are actually more of a snap shot of this. The downside of 2-D plots is of course you need to make compromise. Arbitrary decisions.
For example, consider a simple linear model with a 2-way multiplicative interaction term,
f = xb1 + yb2 + xyb3 + e,
where both x and y are continuous variable.
To present a `marginal effect' of x, that is x's effect on f conditional on y, one need to take a certain difference value (most typically dy/dx). Then you make the case that `when 1 unit changes in x, f changes this much where y values are such and such'. This assumes that x's effect on f is strictly linear: it doesn't matter the change in x we are assuming in the 2d marginal effect figure is from 1 to 2 or 101 to 102. dy/dx assumes it's essentially the same 1-unit change.
Most often, of course, this isn't very realistic. I mean, think of diminishing marginal returns.
One needs to show the whole picture of the structure between f, x, and y just like the picture above to fully explain their relationship.
I know Matlab does it pretty well. Indeed the picture above is generated by Matlab (I believe). But I don't want to learn another package.
Stata has some functions and I tried them today.
One was _graph3d_.
The logic is simply: you have x y and z variables and locate each data point based on them.
The picture I ended up having using my exchange rate regime choice data, though, looks ugly as hell.
This isn't no post-estimation command but I used it as though it was (using predicted values of the DV).
There were, of course, some options to apply, but essentially it does a poor job showing the relationship between variables. Granted, it not like _marginsplot_ where a certain relationship is assigned and simulated, but what was advertised was much more appealing than this ugly picture.
What could've been most useful would be 3d equivalent of _marginsplot_.
Another option, which I see more often these days, is _gr twoway contour_. It should generate something like this:
The figure surely does take into account multi-dimensional variation of data and in some ways much more effective in doing that than 3-d graphs do. It took, however, forever for my macbook pro to generate this with my data (obs=1,510). I needed to go back and forth quite a bit, and if I need to spend an hour every time, this isn't feasible.
-surface- was the third one that I tried. It seemed to have all the same problems that _graph3d_ had. More importantly, it approximates the values when the variable is continuous.
So I gave up there. Spending more than a whole afternoon on a marginally fancy graph that I may or may not use for the paper I'm working on is just insane, I thought.
For now, I would just show two dy/dxs: 1) x's marginal effect conditional on y and 2) y's marginal effect conditional on x.
[method ramble #1] To start.
So it's been a while.
There hasn't simply been an issue I seriously though that I must write something about.
Or more honestly, I have grown increasingly lazier.
Instead of sporadically feeling guilty about a defunct blog, I decide to spend the space on something slightly, like really slightly, more useful.: my method.
I am not a methodologist. I like quant methods. I believe in it. But I simply wasn't trained as a methodologist and don't plan to be in the near future. But at the same time, it's been my obsession to rigorously `spend' the outcomes that methodologists `produced' because doing so seems to be leading to a better science (as well as looking cooler).
I've got a lot to catch up on that front. Methodological advancement political science as a social science field has made is more than astonishing particularly in the past 3-4 years--during which I depleted the usefulness of my outdated method skills.
A few things that I need to really LEARN pretty soon:
1. difference-in-difference
I would've used it for my dissertation if I knew it existed. I was too lazy to know that. I think I get the math, but need to get the hang of it if I want to use it to expand my speculative attacks project.
2. regression discontinuity
Again, I get the math. But need to learn the language.
3. text scraping
There are a few folks who have already well established ways in which researchers scrap data from various sources. I need to have an `original dataset' at some point and this seems to be the closest thing to tap into for now.
4. matching and other causality stuff
I mean, it's a sure thing.
These are long-term goals though. Each task wouldn't really take much time, but I am grappling with a lot of stuff and with the snowcolypse in the DC area, I have been taken hostage at home with kids for the whole first month of the year.
So mostly what I'll be posting here would be day-to-day issues and most likely frustrations I have related to methods (BROADLY DEFINED).
There hasn't simply been an issue I seriously though that I must write something about.
Or more honestly, I have grown increasingly lazier.
Instead of sporadically feeling guilty about a defunct blog, I decide to spend the space on something slightly, like really slightly, more useful.: my method.
I am not a methodologist. I like quant methods. I believe in it. But I simply wasn't trained as a methodologist and don't plan to be in the near future. But at the same time, it's been my obsession to rigorously `spend' the outcomes that methodologists `produced' because doing so seems to be leading to a better science (as well as looking cooler).
I've got a lot to catch up on that front. Methodological advancement political science as a social science field has made is more than astonishing particularly in the past 3-4 years--during which I depleted the usefulness of my outdated method skills.
A few things that I need to really LEARN pretty soon:
1. difference-in-difference
I would've used it for my dissertation if I knew it existed. I was too lazy to know that. I think I get the math, but need to get the hang of it if I want to use it to expand my speculative attacks project.
2. regression discontinuity
Again, I get the math. But need to learn the language.
3. text scraping
There are a few folks who have already well established ways in which researchers scrap data from various sources. I need to have an `original dataset' at some point and this seems to be the closest thing to tap into for now.
4. matching and other causality stuff
I mean, it's a sure thing.
These are long-term goals though. Each task wouldn't really take much time, but I am grappling with a lot of stuff and with the snowcolypse in the DC area, I have been taken hostage at home with kids for the whole first month of the year.
So mostly what I'll be posting here would be day-to-day issues and most likely frustrations I have related to methods (BROADLY DEFINED).
Subscribe to:
Posts (Atom)